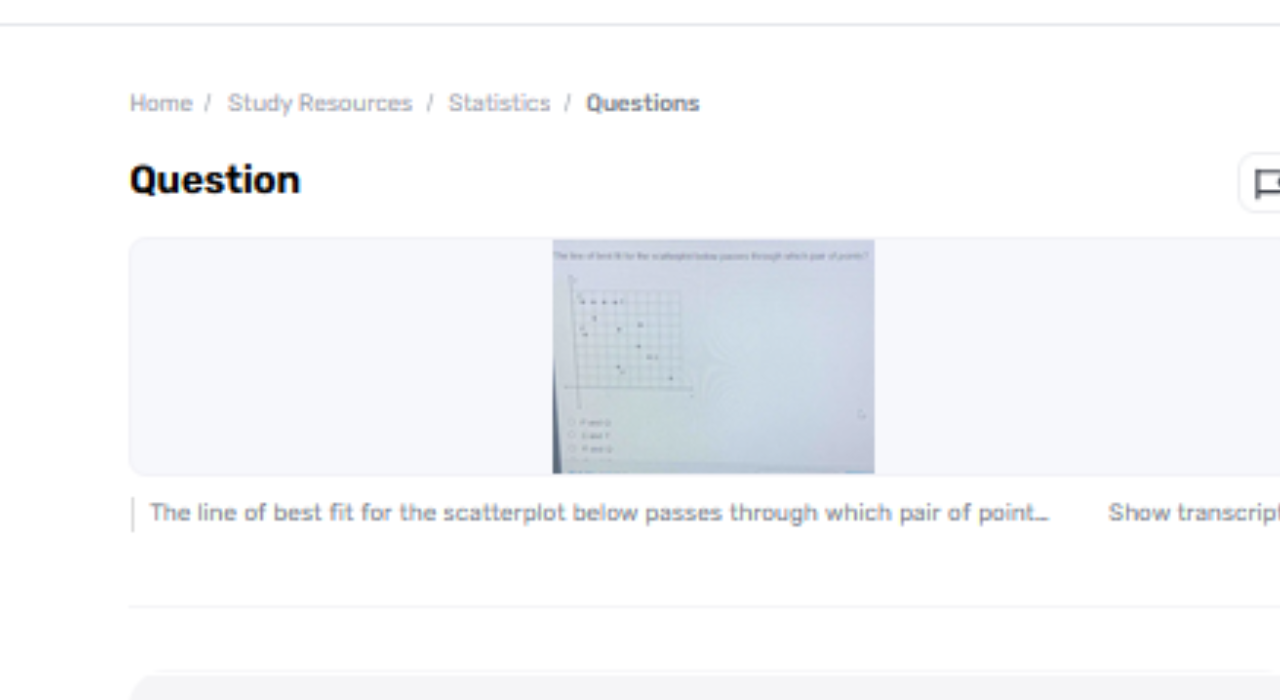
Deciding the line of best fit for a scatterplot includes recognizing a direct condition that best speaks to the information focuses plotted on the chart. This line gives a visual outline of the data’s drift and makes a difference in anticipating values based on the relationship between the factors. To reply to which match of focuses the line of best fit passes through, one must get the method of fitting a line to a scatterplot, analyze the data, and apply measurable strategies to discover the most accurate line. This discourse will direct you through the line of best fit for the scatterplot below passes through which pair of points? these steps to distinguish the right combination of points.
Understanding the Line of Best Fit
The line of best fit, or relapse line, maybe a straight line that best speaks to the relationship between the factors in a scatterplot. It is calculated utilizing the strategy of the slightest squares, which minimizes the whole of the squared contrasts between the watched information focuses and the values anticipated by the line. The objective is to discover the line that has the littlest general blunder in anticipating the subordinate variable based on the free variable. The line of best fit can be communicated by the condition y=mx+b, where mmm is the incline and B is the y-intercept.
Analyzing the Scatterplot
To decide which combination of focuses the line of best fit passes through, begin by looking at the scatterplot. Recognize the common slant of the information points: does the information appear a positive or negative relationship? Are there any self-evident clusters or exceptions? By plotting these focuses on a chart, you’ll be able to outwardly assess the line that best fits the information. Regularly, the line of best fit will not pass precisely through any of the focuses but will be as near as conceivable to all of them. In any case,
Calculating the Line of Best Fit
To decide the line of best fit, utilize measurable strategies or computer program instruments to perform a direct relapse examination. This handle includes calculating the incline mmm and y-intercept b of the line utilizing equations determined from the information. For a set of information points (x1,y1),(x2,y2)-¦,(xn,yn)(x_1, y_1), (x_2, y_2), dots, (x_n, y_n)(x1,y1),(x2,y2)-,(xn,yn), the incline mmm is given by: m=n-xi2-(-xi)2n-(xiii)-xi-yi The y-intercept b is calculated utilizing the: b=n-y-m-xi Once you have got the condition of the line, you’ll decide which of the information focuses it passes through precisely by substituting the x-values of the focuses into the condition and checking in case the calculated y-values coordinate the y-values of the focuses.
Confirming the Match of Focuses
After deciding the condition of the line of best fit, substitute the x-coordinates of the given sets of focuses into the line’s condition to check on the off chance that they fulfill the condition. For each combination, calculate the comparing value and compare it with the genuine y-coordinate of the point. In case a match of focuses fulfills the line condition, at that point the line of best fit passes through these focuses.
Steps for Reacting to a Gauth Request
1. Interpret the Inquiry:
Determine if it relates to setup, utilization, administration, or investigation.
2. Collect Information:
Audit Gauth official documentation and common client challenges.
3. Draft the Reply:
Orchestrate key data clearly and directly.
4. Verify and Refine:
Check for exactness and clarity, guaranteeing the reaction is brief and relevant.
Conclusion
Distinguishing the match of focuses that the line of best fit passes through includes understanding the concept of the line of best fit, analyzing the scatterplot, calculating the relapse line, and confirming particular focuses. The line of best fit gives a direct representation of the information and makes a difference in making expectations and understanding patterns. By applying factual strategies to calculate and confirm the line condition, one can precisely decide which match of focuses the line converges. This handle highlights the significance of exact calculations and confirmation in analyzing information and making educated choices based on measurable models.